루트가 무엇인지!
루트는 쉽게얘기해서 어떤 수를 제곱해서 다른 수를 만드는 수이다.

에서 x는 a의 제곱근이라고 합니다.

와 같은 이야기 입니다.
-루트의 기호랑 의미
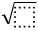
는 우리말로 제곱근이라고 하며. 어떤 수 x를 제곱하여 나온 수를 a라 할때 a는 제곱수, x를 제곱근이라고 합니다.
-루트를 이용하여 푸는 문제
루트를 이용해서 푸는 문제는 다방면으로 많습니다.
그중 가장 실수를(제 경험으로는)많이 하는 부분이 유리화 시키는 부분입니다.
루트가 씌워져 있는 것 중 유리수가 아닌 수를 무리수라합니다.
그런 유리수와 무리수를 합쳐 실수라 합니다.
그래서 벤다이어 그램으로 생각해 보면
자연수를 정수가 포함하고, 정수를 유리수가 포함하고 유리수를 실수가 포함하는데 실수지만 유리수가 아닌 수를 무리수라고 합니다.
그 무리수는 제곱근이 있는 수입니다만, 물론 유리수가 아니어야 합니다.
-계산방법을 기초~심화까지.
1.  일때 X의 값
일때 X의 값
어떤 수를 제곱하면 4 이므로
 이므로
이므로
x=2
2.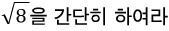
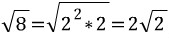
주의 -> 근호밖으로 수를 빼낼 때는 제곱인 수를 빼야 합니다.
즉 2가 나온 이유는  이므로 2가 빠져나온 것입니다.
이므로 2가 빠져나온 것입니다.
다른 예로는

등이 있고.
제가 아까 언급했던 유리화를 하겠습니다.
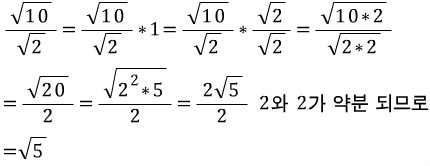
이건 유리화에서 살짝 업그레이드(해봤자 약분)인데 유리수의 모양이  의 모양인것은 아시죠? 근데 거기서 a는 정수여야 하는데
의 모양인것은 아시죠? 근데 거기서 a는 정수여야 하는데  는 무리수 이므로 이 수를 바꿔줘야 합니다. 그런데 여기다가 1을 곱하면 값은 그대로 이므로
는 무리수 이므로 이 수를 바꿔줘야 합니다. 그런데 여기다가 1을 곱하면 값은 그대로 이므로 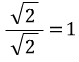 를 곱해서
를 곱해서  를 없애는 것이죠. 그러면서 위의 루트 10도 곱해져서 루트 20이 된것이고 루트 20을 보기좋게 정리하다보니 분모와 약분되는 것입니다.
를 없애는 것이죠. 그러면서 위의 루트 10도 곱해져서 루트 20이 된것이고 루트 20을 보기좋게 정리하다보니 분모와 약분되는 것입니다.
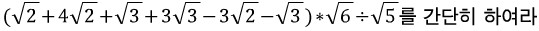
제곱근이 있는 수의 덧셈 뺄셈은 문자 계산법과 동일시 하시면 됩니다.
루트 안에 있는 수가 같은 것 끼리 계산하시면 됩니다.
곱셈은 조금 다릅니다. 곱셈은 루트는 그대로 두고 루트끼리 곱하시면 되구요. 나누기는 역수를 곱하는 방식으로 하시면 됩니다. 만약 나누기가 약분이 되지 않을 때가 있습니다. 그때는 끝에 유리화까지 시켜주셔야 완벽한 답이 됩니다.

조금 어렵게 느껴질지도 모르지만... 아직 심화에 들어가지 않았다;;
여기까지가 기초구요. 이제 살짝 심화.

특히 정수부분과 소수부분을 이용한 문제는 수도 없이 많이 나오므로 솔직히 중요한 개념이기도 합니다.
그다음은 도형문제도 조금 있지만 도형은 생략하기로 하죠. 기본기만 있다면 도형은 쉽게 할 수 있기 때문입니다.
그럼 심화문제 들어갑니다.
아... 그렇게 어렵지는 않을 겁니다.

'Basics > Mathmatics' 카테고리의 다른 글
| 수학기호 (0) | 2014.06.09 |
|---|---|
| 부채꼴의 넓이, 반지름, 호의 길이, 중심각 (0) | 2014.06.09 |
| 직선의 방정식 (0) | 2014.06.09 |
| 길이단위환산 (0) | 2014.06.09 |
| 행렬의 곱 (0) | 2014.06.09 |